Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- Dense_Rank
- 상관관계
- 데이터분석
- 회귀분석
- 그래프시각화
- Sum
- 정보획득량
- 불순도제거
- count
- 빅데이터
- 그래프 생성 문법
- 히스토그램 그리기
- 단순회귀 분석
- max
- 데이터분석가
- 팀스파르타
- sql
- if문 작성법
- 회귀분석 알고리즘
- loop 문
- 순위출력
- 총과 카드만들기
- difftime
- Intersect
- sqld
- 막대그래프
- 여러 데이터 검색
- merge
- %in%
- 빅데이터분석
Archives
- Today
- Total
ch0nny_log
[빅데이터분석] R _ 70. ROC 커브와 cut-off 본문
■ K-means 쪽지시험 문제 풀이
#1. 데이터 구성하기 data3 <- data.frame( 학생 = c("학생1","학생2","학생3","학생4","학생5"), 국어 = c(83,87,63,92,71), 영어 = c(78,82,67,89,69), 수학 = c(92,88,72,94,77), 과학 = c(86,91,66,96,73) ) data3 data3_no_id <- data3[ , -1] data3_no_id #2. k-means 클러스터링 수행하기 set.seed(123) kmeans_result3 <- kmeans(data3_no_id,centers=2, nstart=25) kmeans_result3 #3. 각 클러스터의 중심 좌표 출력하기 kmeans_result3$centers #4. 각 클러스터에 속한 학생 출력하기 data3$cluster <- kmeans_result3$cluster data3


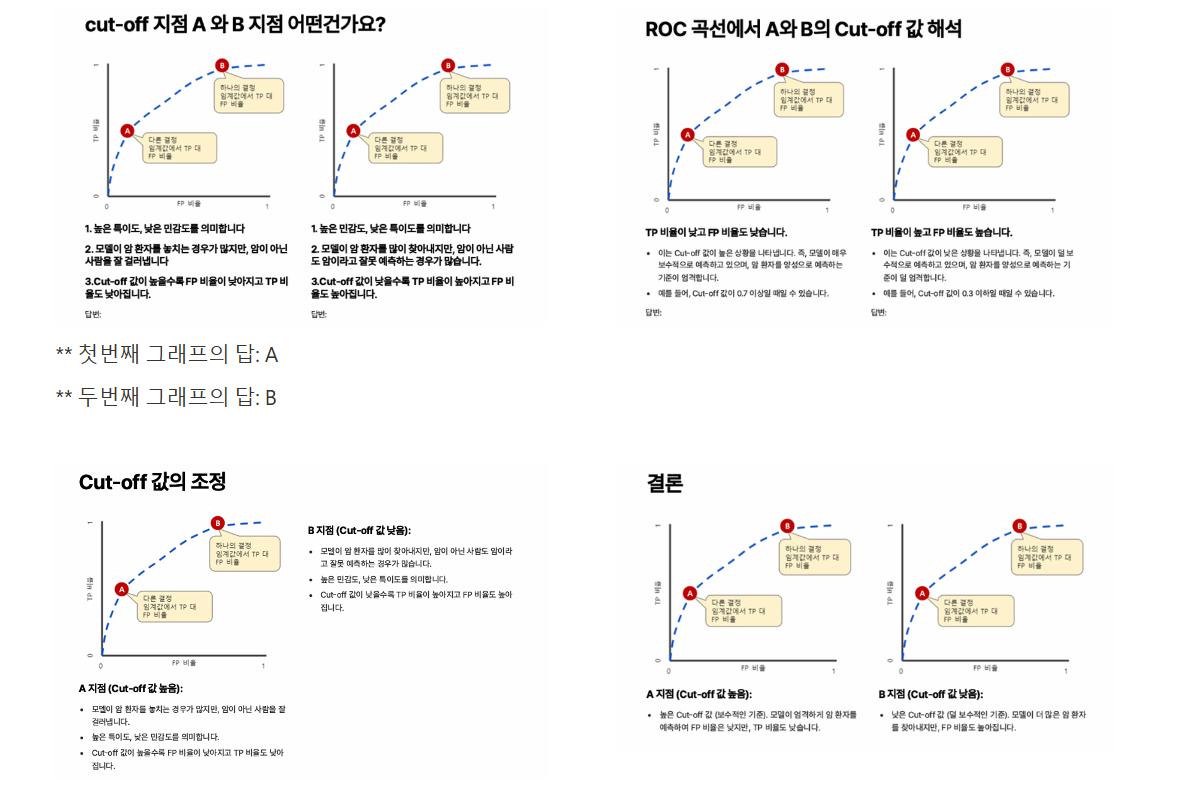
** 파란색 곡선이 가장 좋은 모델임. 라인이 파란색 쪽으로 갈 수록 좋은 모델이고 대각선 쪽으로 갈 수록 분류를 잘하지 못한하는 모델을 나타냄.
** x 축 → 민감도 / y 축 → 1 - 특이도



실습. 독일 은행 은행 대출금 불이행자 예측 모델 만들기
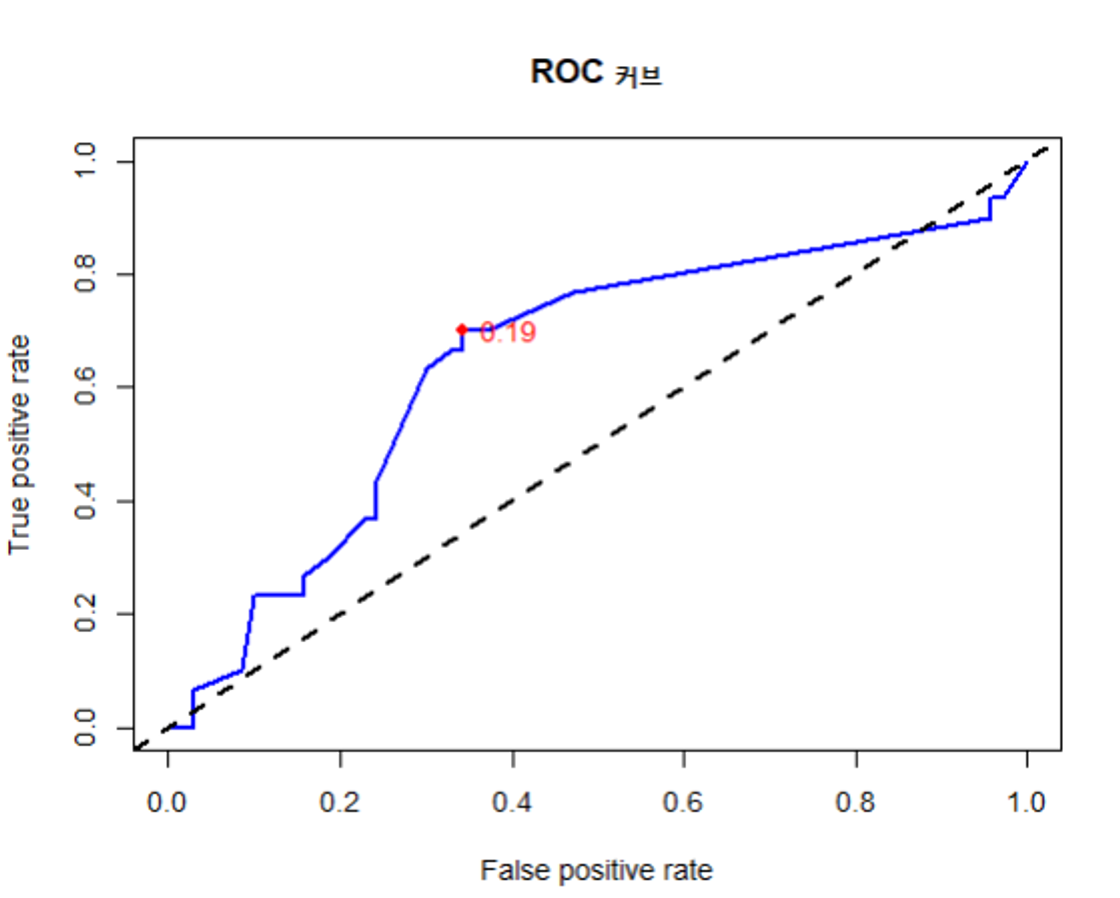
# 데이터 로드 credit <- read.csv("c:\\data\\credit.csv", stringsAsFactors=TRUE) # 결측치 확인 colSums(is.na(credit)) # 데이터 분할 library(caret) set.seed(1) k <- createDataPartition(credit$default, p=0.9, list=F) train_data <- credit[k, ] test_data <- credit[-k, ] # 모델 생성 및 훈련 #install.packages("C50") library(C50) credit_model <- C5.0(train_data[, -17], train_data[, 17]) # 모델 예측 result <- predict(credit_model, test_data[, -17]) # 모델 평가 accuracy <- sum(result == test_data[, 17]) / 100 accuracy # 0.67% -> 의사결정나무 1개로 예측한 것이기 때문에 정확도가 낮을 수 밖에 없음. # ROC 곡선 그리기 credit_test_prob <- predict(credit_model, test_data[, -17], type="prob") # type="prob" -> 확률이 출력되도록 함. => 확률 정보가 있어야 ROC 곡선을 그릴 수 있음. credit_results <- data.frame( actual_type = test_data[, 17], # 정답 predict_type = result, # 예측값 prob_yes = round(credit_test_prob[, 2], 5), # 채무 불이행할 확률 prob_no = round(credit_test_prob[, 1], 5) # 채무 이행할 확률 ) # 민감도, 특이도, 정밀도 계산(ROC 곡선을 그릴 때 꼭 필요한 데이터는 아니지만 ROC 곡선과 함께 결과로 보여줘야하는 데이터이기 때문에 출력하는 것임.) library(caret) sensitivity(credit_results$predict_type, credit_results$actual_type, positive='yes') # 민감도: 0.266(암환자를 암환자로 잘 예측한 비율 -> 환자입장) specificity(credit_results$predict_type, credit_results$actual_type, negative='no') # 특이도: 0.842(정상환자를 정상환자로 잘 예측한 비율 -> 환자입장) posPredValue(credit_results$predict_type, credit_results$actual_type, positive='yes') # 정밀도: 0.421(모델이 암환자로 예측한 환자 중 실제 암환자인 비율 -> 모델입장) # ROC 곡선 그리기 install.packages("ROCR") library(ROCR) pred <- prediction(predictions = credit_results$prob_yes, labels = credit_results$actual_type) perf <- performance(pred, measure = "tpr", x.measure = "fpr") plot(perf, main = "ROC 커브", col = "blue", lwd = 2) abline(a = 0, b = 1, lwd = 2, lty = 2) perf # 26 개의 데이터 포인트를 찾았음을 알 수 있음. # AUC 계산 value <- performance(pred, measure = "auc") auc <- unlist(value@y.values) auc # 0.64 -> 1에 가까울 수록 좋은 모델임. # 최적의 Cut-off 지점 찾기 cutoff_data <- data.frame(cut = perf@alpha.values[[1]], tpr = perf@y.values[[1]], fpr = perf@x.values[[1]]) cutoff_data # cut-off 값, tpr 과 fpr 데이터를 추출해서 cutoff_data 라는 데이터프레임 생성. cutoff_data$distance <- cutoff_data$tpr - cutoff_data$fpr # tpr 에서 fpr 을 뺀 값인 distance 라는 컬럼을 추가함. 최적의 cut-off 지점이 distance 값이 최대가 되는 지점임. optimal_cutoff <- cutoff_data[which.max(cutoff_data$distance), "cut"] optimal_cutoff # 0.191 # 최적의 Cut-off 지점 시각화 optimal_tpr <- cutoff_data[which.max(cutoff_data$distance), "tpr"] optimal_fpr <- cutoff_data[which.max(cutoff_data$distance), "fpr"] optimal_tpr # 0.7 -> 최적의 cut-off 지점의 tpr(y축) 값 optimal_fpr # 0.34 -> 최적의 cut-off 지점의 fpr(x축) 값 # ROC 곡선 그리기 및 cut-off 지점 포인트 찍기 plot(perf, main = "ROC 커브", col = "blue", lwd = 2) abline(a = 0, b = 1, lwd = 2, lty = 2) points(optimal_fpr, optimal_tpr, col = "red", pch = 19) text(optimal_fpr, optimal_tpr, labels = round(optimal_cutoff, 2), pos = 4, col = "red")
문제. 빅분기 대비
1. 데이터 로드 및 전처리
유방암 데이터를 로드하고 전처리하십시오. 불필요한 id 컬럼을 제거하고 diagnosis 컬럼을 factor 타입으로 변환하시오.
data <- read.csv('c:\\data\\wisc_bc_data.csv', stringsAsFactors = TRUE) head(data) data <- data[ , -1] data$diagnosis <- as.factor(data$diagnosis) str(data)2.데이터 분할
훈련 데이터(90%) 와 테스트 데이터(10%) 로 나누시오.
library(caret) set.seed(1) k <- createDataPartition(data$diagnosis, p = 0.9, list = F) train_data <- data[ k, ] test_data <- data[ -k, ] nrow(train_data) # 513 nrow(test_data) # 56
3. 모델 생성 및 훈련
C5.0 알고리즘을 사용하여 의사결정트리 모델을 생성하고 훈련하시오.
library(C50) wisc_model <- C5.0(train_data[, -1], train_data[ , 1])4. 모델예측
훈련된 모델을 사용하여 테스트 데이터에 대해 예측하시오.result <- predict(wisc_model, test_data[, -1])5. 모델 평가
accuracy <- sum(result == test_data[ , 1])/ nrow(test_data) accuracy # 0.986. ROC 곡선그리기
# ROC 곡선 그리기 wisc_test_prob <- predict(wisc_model, test_data[, -1], type="prob") # type="prob" -> 확률이 출력되도록 함. => 확률 정보가 있어야 ROC 곡선을 그릴 수 있음. wisc_results <- data.frame( actual_type = test_data[, 1], # 정답 predict_type = result, # 예측값 prob_M= round(wisc_test_prob[, 2], 5), # 암일 확률 prob_B = round(wisc_test_prob[, 1], 5) # 정상일 확률 ) # 민감도, 특이도, 정밀도 계산(ROC 곡선을 그릴 때 꼭 필요한 데이터는 아니지만 ROC 곡선과 함께 결과로 보여줘야하는 데이터이기 때문에 출력하는 것임.) library(caret) sensitivity(wisc_results$predict_type, wisc_results$actual_type, positive='M') specificity(wisc_results$predict_type, wisc_results$actual_type, negative='B') posPredValue(wisc_results$predict_type, wisc_results$actual_type, positive='M') # ROC 곡선 그리기 install.packages("ROCR") library(ROCR) pred <- prediction(predictions = wisc_results$prob_M, labels = wisc_results$actual_type) perf <- performance(pred, measure = "tpr", x.measure = "fpr") plot(perf, main = "ROC 커브", col = "blue", lwd = 2) abline(a = 0, b = 1, lwd = 2, lty = 2) perf # 26 개의 데이터 포인트를 찾았음을 알 수 있음. # AUC 계산 value <- performance(pred, measure = "auc") auc <- unlist(value@y.values) auc # 0.977. Cut-off 지점 찾기
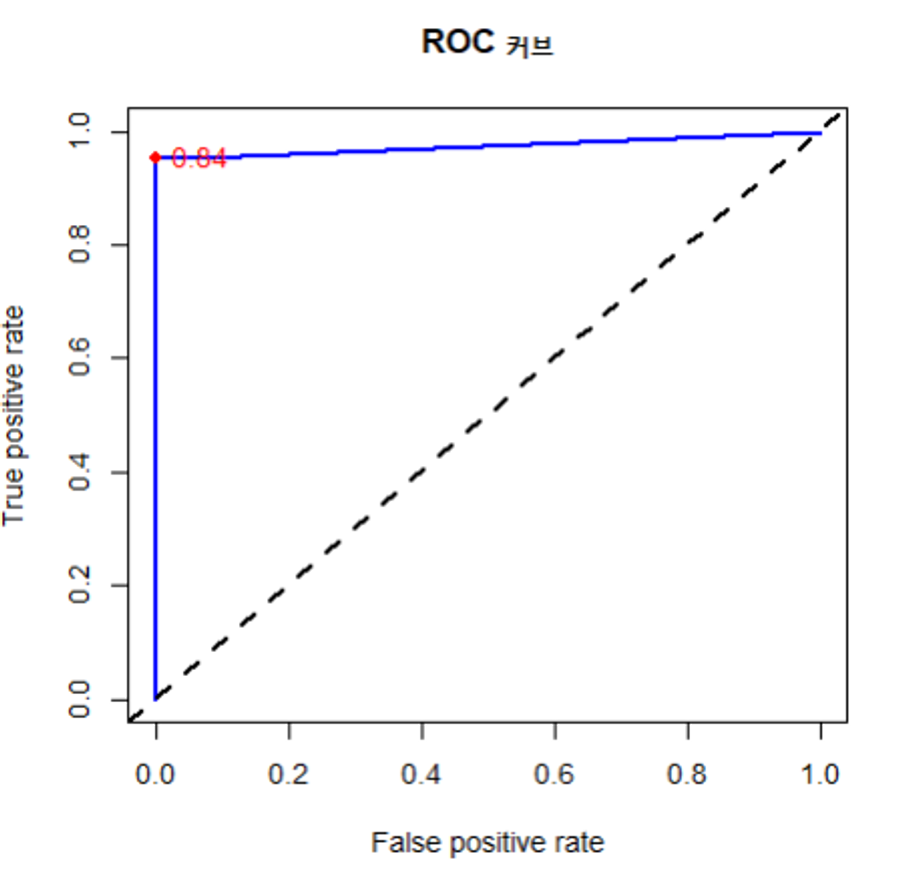
# 최적의 Cut-off 지점 찾기 cutoff_data <- data.frame(cut = perf@alpha.values[[1]], tpr = perf@y.values[[1]], fpr = perf@x.values[[1]]) cutoff_data # cut-off 값, tpr 과 fpr 데이터를 추출해서 cutoff_data 라는 데이터프레임 생성. cutoff_data$distance <- cutoff_data$tpr - cutoff_data$fpr # tpr 에서 fpr 을 뺀 값인 distance 라는 컬럼을 추가함. 최적의 cut-off 지점이 distance 값이 최대가 되는 지점임. optimal_cutoff <- cutoff_data[which.max(cutoff_data$distance), "cut"] optimal_cutoff # 0.191 # 최적의 Cut-off 지점 시각화 optimal_tpr <- cutoff_data[which.max(cutoff_data$distance), "tpr"] optimal_fpr <- cutoff_data[which.max(cutoff_data$distance), "fpr"] optimal_tpr # 0.84 -> 최적의 cut-off 지점의 tpr(y축) 값 optimal_fpr # 0.95 -> 최적의 cut-off 지점의 fpr(x축) 값 # ROC 곡선 그리기 및 cut-off 지점 포인트 찍기 plot(perf, main = "ROC 커브", col = "blue", lwd = 2) abline(a = 0, b = 1, lwd = 2, lty = 2) points(optimal_fpr, optimal_tpr, col = "red", pch = 19) text(optimal_fpr, optimal_tpr, labels = round(optimal_cutoff, 2), pos = 4, col = "red")
'빅데이터 분석(with 아이티윌) > R' 카테고리의 다른 글
| [빅데이터분석] R _ 72. 앙상블 (0) | 2024.07.30 |
|---|---|
| [빅데이터분석] R _ 71. k-foldout (0) | 2024.07.30 |
| [빅데이터분석] R _ 69. 모델 평가 (1) | 2024.07.26 |
| [빅데이터분석] R _ 68. K-means 알고리즘 (0) | 2024.07.26 |
| [빅데이터분석] R _ 67. 연관 분석 (0) | 2024.07.25 |