| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 순위출력
- 데이터분석가
- 불순도제거
- if문 작성법
- 총과 카드만들기
- 회귀분석 알고리즘
- 회귀분석
- merge
- Intersect
- 그래프 생성 문법
- 그래프시각화
- %in%
- 빅데이터
- 빅데이터분석
- 팀스파르타
- sql
- 데이터분석
- 여러 데이터 검색
- count
- max
- Sum
- 히스토그램 그리기
- Dense_Rank
- sqld
- loop 문
- 단순회귀 분석
- difftime
- 정보획득량
- 상관관계
- 막대그래프
- Today
- Total
ch0nny_log
[빅데이터분석] R _ 58. 단순 회귀분석 알고리즘 본문
simple_regrression <- function(x_num) {
x= c(2,4,6,8,10)
y= c(50,55,60,65,70)
W= cov(x,y)/var(x) #기울기
b= mean(y)-W*mean(x) #절편
y_hat= W*x_num + b #회귀직선의 방정식
print(y_hat)
}
simple_regrression(9)


골턴이라는 학자가 회귀를 발견했는데 몇 세대에 걸쳐서 사람들의 키를 조사했습니다.
키가 점점 세대가 지날 수록 평균으로 회귀(돌아감) 하는것을 발견했습니다.


단순 회귀분석 이해할 때 꼭 알아야하는 수학용어 2가지?
1. 공분산
(두변수가 함께 어떻게 변화하는지의 지표)
2. 분산
(데이터들이 평균으로 부터 얼마나 떨어져 있는지의 지표)
※ (질문1) 회귀식을 도출할 때 공분산이 필요한 이유?
공분산은 두 변수가 함께 어떻게 변하는지를 측정하는 지표입니다. 두 변수가 어떤 관계를 가지는지, 즉 하나의 변수가 증가할 때 다른 변수가 어떻게 변하는지를 알려줍니다. 공분산의 값이 양수인지 음수인지에 따라 두 변수 간의 관계를 알 수 있습니다.
공분산의 값에 따른 해석
-
- 예를 들어, 아이스크림 판매량과 기온의 관계를 생각해 봅시다. 날씨가 더워질수록 아이스크림 판매량이 증가하는 경향이 있습니다.
- 기온이 올라갈 때 아이스크림 판매량도 함께 증가합니다.
- 이러한 경우 공분산은 양의 값을 가지게 됩니다.
- 즉, 하나의 변수가 증가할 때 다른 변수도 증가하는 관계를 나타냅니다.
- 예를 들어, 운동량과 체중의 관계를 생각해 봅시다. 운동량이 증가할수록 체중이 감소하는 경향이 있을 수 있습니다.
- 운동을 많이 할수록 체중이 줄어드는 경우가 많습니다.
- 이러한 경우 공분산은 음의 값을 가지게 됩니다.
- 즉, 하나의 변수가 증가할 때 다른 변수는 감소하는 관계를 나타냅니다.
※ 쉬운 예시로 설명하기
양의 공분산 예시
- 기온과 아이스크림 판매량:
- 날씨가 더워지면 아이스크림을 더 많이 먹고 싶어져서 판매량이 증가합니다.
- 기온이 30도일 때 100개의 아이스크림이 팔리고, 35도일 때 150개의 아이스크림이 팔린다고 합시다.
- 기온이 증가함에 따라 아이스크림 판매량도 함께 증가하는 것을 볼 수 있습니다.
- 이처럼 기온과 아이스크림 판매량은 같은 방향으로 변하므로, 이 둘 사이의 공분산은 양의 값을 가집니다.
음의 공분산 예시
- 운동량과 체중:
- 운동을 많이 할수록 체중이 줄어드는 경향이 있을 수 있습니다.
- 한 사람이 매일 1시간씩 운동할 때 체중이 70kg에서 68kg로 줄어든다고 합시다.
- 매일 2시간씩 운동할 때 체중이 68kg에서 65kg로 더 줄어들 수 있습니다.
- 운동량이 증가함에 따라 체중이 감소하는 것을 볼 수 있습니다.
- 이처럼 운동량과 체중은 반대 방향으로 변하므로, 이 둘 사이의 공분산은 음의 값을 가집니다.
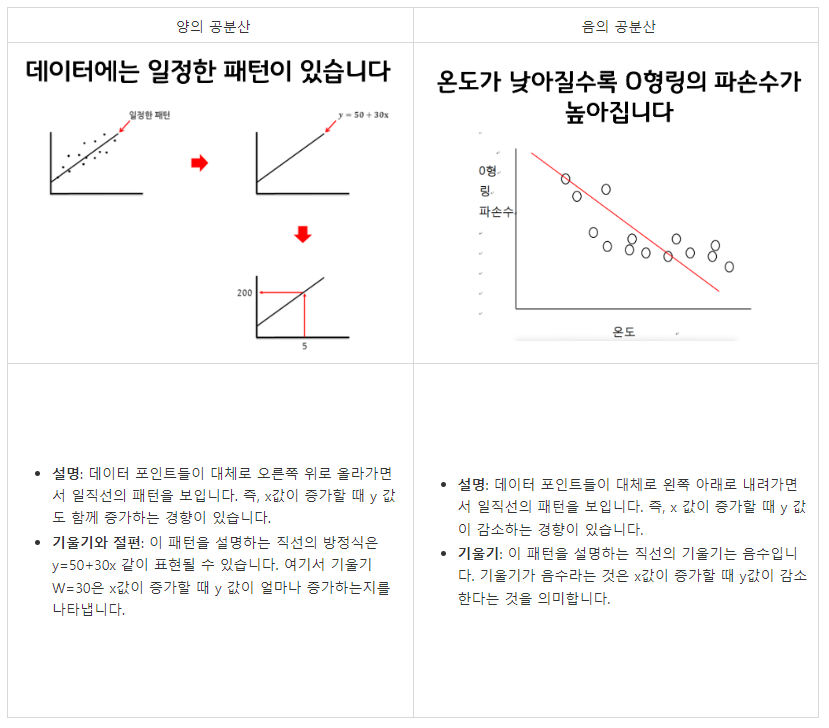
※ (질문2) 공분산을 분산으로 나누면 왜 기울기가 나오는가?
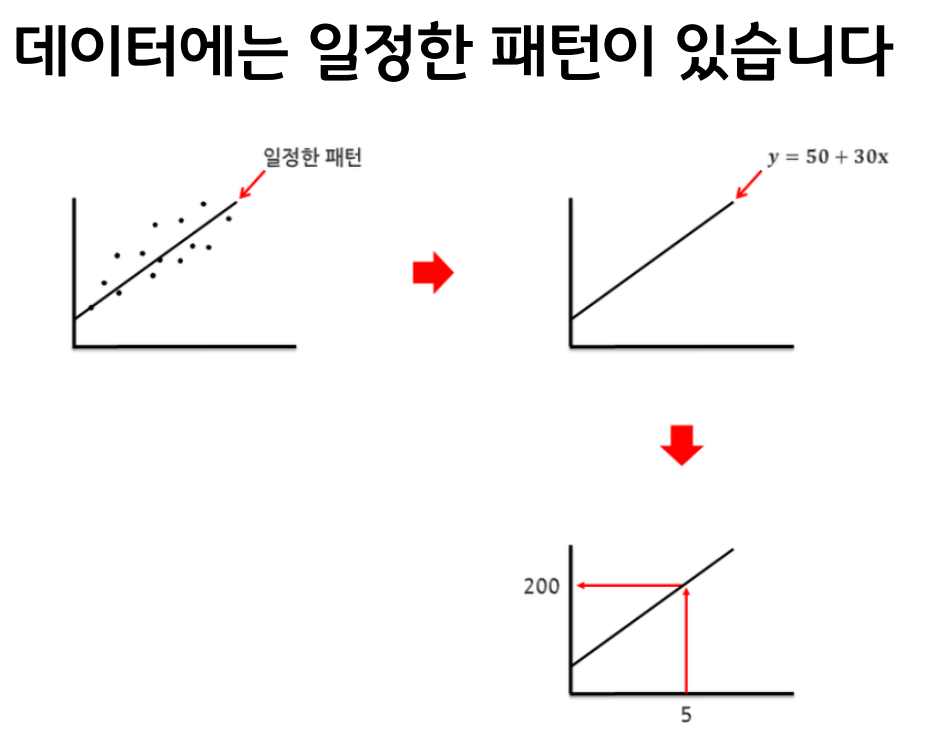

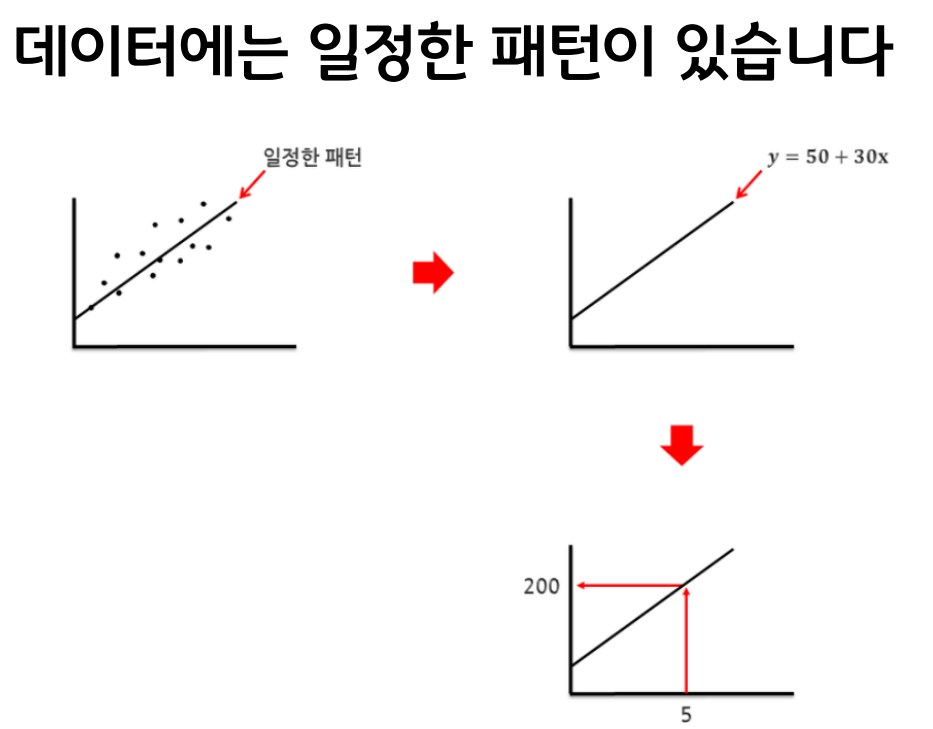
※ (질문3) 단순회귀 직선의 방정식에 절편 구하는 방법 ?

+ 온도에 따른 아이스크림 판매량
x: 온도
y: 아이스크림 판매량
기울기 : 공분산/ 분산 = cov(x, y) / var(x)
b: 절편

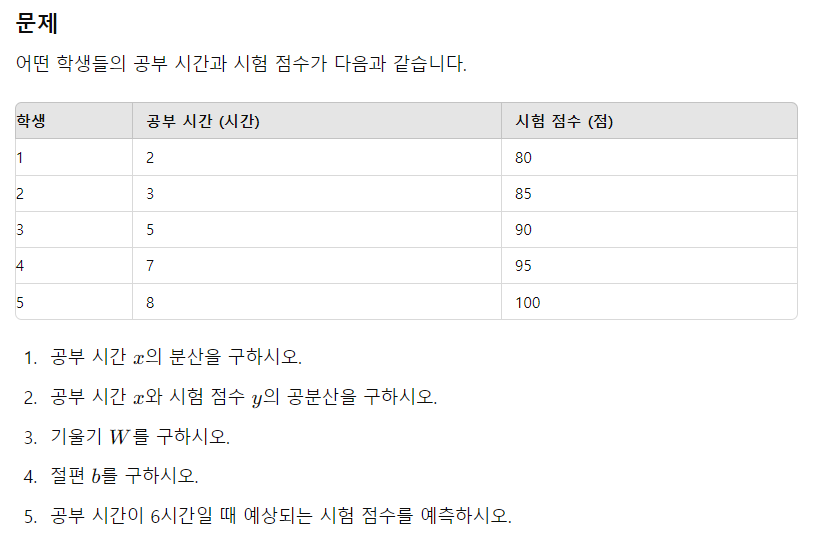



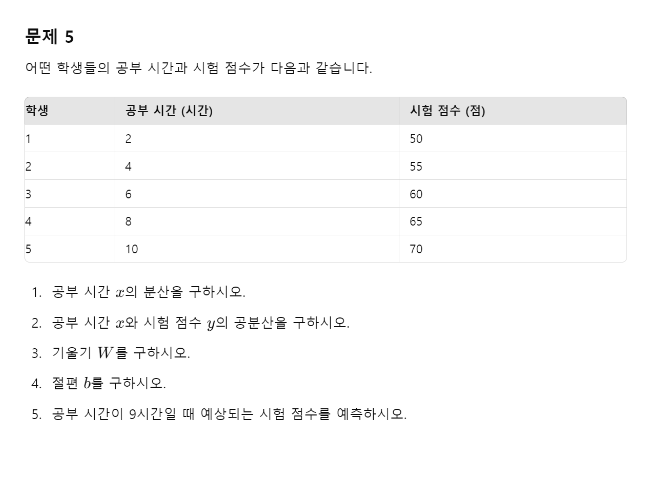

실습1. 위 문제를 R을 사용하여 기울기와 절편을 구해서 회귀식을 도출하는 아래의 함수를 생성하시오.
simple_regression <- function(x_num) { x= c(2,4,6,8,10) y= c(50,55,60,65,70) W = cov(x,y) / var(x) # 기울기 b = mean(y) - W * mean(x) # 절편 y_hat = W*x_num + b # 회귀직선의 방정식 list( W= W, b=b, y_hat=y_hat) } result <- simple_regression(9)
※ 단순회귀식을 쉽게 추출하는 R 내장함수인 lm 이용하는 방법
#1. 데이터를 구성합니다. data <- data.frame( 학생= c(2,4,6,8,10), 공부시간= c(1,2,4,6,7), 시험점수= c(50,55,60,65,70) ) print(data) #2. lm 함수로 회귀식을 도출합니다. model <-lm(시험점수~공부시간, data=data) summary(model)b= 절편 / w= 기울기
※ lm함수를 이용해서 단순 회귀식을 만들고 시각화하기
주제: 사료의 탄닌 함유량과 애벌레 성장간의 관계에 대한 회귀식 도출#1. 데이터 로드 reg <-read.table('c:\\data\\regression.txt', header=T) reg #2. 산포도 그래프 attach(reg) plot(growth~tannin, data = reg, pch=21, col ='skyblue',bg='skyblue',cex=2) ## 설명: plot(y~x, data=데이터 프레임명) #3. 회귀분석을 통해 회귀계수 절편 도출 model <- lm(growth~tannin, data=reg) model #4. 산포도그래프와 회귀직선을 겹쳐 시각화 attach(reg) plot(growth~tannin, data = reg, pch=21, col ='skyblue',bg='skyblue',cex=2) model <- lm(growth~tannin, data=reg) abline(model,col='coral')산포도 그래프 절편 도출
■ 잔차
- 표본에서 실제값이 회귀선(모델예측값)과 비교 했을 때의 차이
#5. 잔차 생성 *결정계수외에 다른 성능 척도를 설명해줘야 그 모델에 대한 신뢰가 일어남
y_hat <- predict(model, tannin=tannin) #훈련데이터로 예측값 출력
join<- function(i) #join이라는 함수를 생성
lines(c(tannin[i],tannin[i]),c(growth[i],y_hat[i]),col='green')
sapply(1:9, join) #sapply 함수는 join 함수에 숫자 1~9까지를 제공함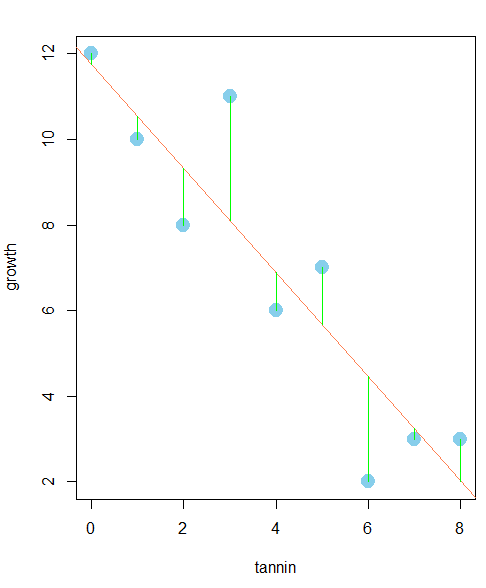
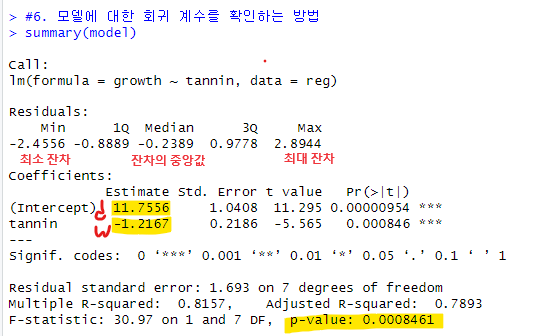
잔차는 실제값과 모델의 예측값의 차이임. 이 값들이 클수록 모델의 예측이 실제값과 많이 다르다는 것을 의미함
기울기: -1.2167/ 절편: 11.7556 / 표준오차: 1.0408 / p-value: 0.000846으로 0.05 보다 작기 때문에 이 기울기가 통계적으로 유의미하다는 것을 의미함
+) p-value (가설검증시 중요한 데이터)
*** 면 p값: 0.001 이하
** 면 p값: 0.01 이하
* 면 p값: 0.05 이하
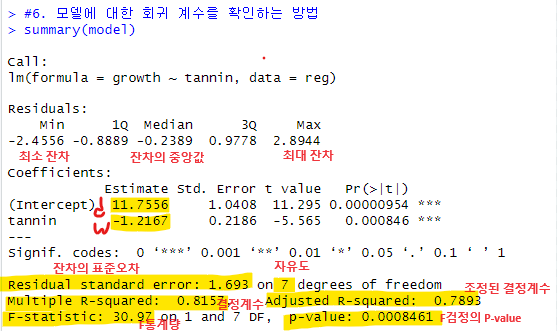
* 잔차의 표준오차 : 1.693
잔차의 표준오차는 모델의 예측값이 실제 관측값과 평균적으로 얼마나 벗어나는지를
나타냅니다. 모델이 예측한값이 실제값으로 부터 평균적으로 1.693 만큼 벗어났음을
의미합니다. 잔차의 표준오차가 작을 수록 모델이 데이터를 더 잘 설명하고 있음을
뜻합니다.
* 결정계수가 0.8157 이 출력되고 있습니다. 이 값이 1에 가까울수록 모델의
설명력이 높음을 의미합니다.
* 조정된 결정계수: 0.7893 조정된 결정계수가 결정계수의 차이가 적을수록 좋은 모델입니다. 독립변수들의 갯수가 많으면 결정계수가 높아지는데 조정된 결정계수는
독립변수들이 많다고 해서 같이 높아지지 않습니다. 독립변수들이 많으면 복잡한 모델이
됩니다.
* F-statistic : F 통계량으로 회귀모델의 전반적이 유의성을 검정합니다.
* p-value : F 검정의 p-value 값. 통계적으로 유의미한 값이 출력되고 있음.
실습2. 광고비와 매출간의 단순 회귀 분석모델을 생성하고 회귀 계수를 출력하시오.
# 1. 데이터 로드 simple_hg <- read.csv("c:\\data\\simple_hg.csv") simple_hg # 2. 산포도 그래프 attch(simple_hg) plot(input ~ cost, data=simple_hg, pch=21, col='orange',bg='yellow', cex=1.5) # 3. 회귀분석해서 기울기와 절편 구하기 model <- lm(input ~ cost, data=simple_hg) model # 4. 2번에서 시각화한 산포도 그래프에 회귀직선 겹쳐 그리기 attch(simple_hg) plot(input ~ cost, data=simple_hg, pch=21, col='orange',bg='yellow', cex=1.5) model <- lm(input ~ cost, data=simple_hg) abline(model, col='red') title('광고비가 매출에 미치는 영향')
실습 2_1. 위 모델의 성능을 해석하시오.
summary(model)회귀식 : y = 2.18 x + 62.92
결정계수 0.78
p value 값이 0.000099 (통계적으로 유의한 결과)
-> 광고비가 100만원에서 100.5 만으로 증가하면 매출액은 1.0993225 단위만큼 증가합니다.
회귀식 : y = 2.18 x + 62.92
1. 광고비가 1단위 증가할때 매출액은 2.1865 단위로 증가합니다.
2.1865의 단위가 1억이라고 가정하면
2. 광고비가 10단위 증가할때 매출액은 21.865 단위로 증가 합니다.
광고비가 100만원 증가하면 매출액이 218.65 억원이 증가합니다.
광고비가 200만원 증가하면 매출액이 437.3억원이 증가합니다.
광고비가 300만원 증가하면 매출액이 655.95억이 증가합니다.
실습3. 미국 우주 왕복선 챌린져호의 폭파 원인을 단순회귀 분석으로 분석하시오 !코드순서:
#1. 데이터 불러오기
#2. 데이터로 산포도 그래프 그리기
#3. 단순회귀 분석하기
#4 2번에서 시각화한 산포도 그래프에 회귀직선 겹쳐 그리기
#5. 단순회귀분석 결과 해석하기
코드구현:
#1. 데이터 불러오기 cha <- read.csv("c:\\data\\challenger.csv") cha #2. 데이터로 산포도 그래프 그리기 attch(cha) plot(distress_ct ~ temperature, data=cha, pch=21, col='orange',bg='yellow', cex=1.5) #3. 단순회귀 분석하기 #절편: 3.69841 / 기울기:-0.04754 model <- lm(distress_ct ~ temperature, data=cha) model # 4. 2번에서 시각화한 산포도 그래프에 회귀직선 겹쳐 그리기 attch(simple_hg) plot(distress_ct ~ temperature, data=cha, pch=21, col='orange',bg='yellow', cex=1.5) model <- lm(distress_ct ~ temperature, data=cha) abline(model, col='red') title('온도가 o링 파손수에에 미치는 영향') #5. 단순회귀분석 결과 해석하기 summary(model)단순회귀식: y= 0.0047*x + 3.69841 (y= o형파손수, x= 온도)
2.21개 31도 F(화씨)
0.82개 60도 F(화씨)
0.34개 70도 F(화씨)
-> 화씨 30도에서 발사하는게 화씨 60도에서 발사하는 것 보다 3배 더 위험하고 70도에서 발사하는 것보다 7~8배위험하다.
실습 4. 키와 체중과의 단순회귀 분석을 하시오. (키-독립변수/ 체중- 종속변수 )
#1. 데이터 불러오기 # 데이터 생성 weight <- c(72, 72, 70, 43, 48, 54, 51, 52, 73, 45, 60, 62, 64, 47, 51, 74, 88, 64, 56, 56) tall <- c(176, 172, 182, 160, 163, 165, 168, 163, 182, 148, 170, 166, 172, 169, 163, 170, 182, 174, 164, 160) # 데이터 프레임 생성 df <- data.frame(weight, tall) # 데이터 프레임 출력 print(df) #2. 데이터로 산포도 그래프 그리기 attch(df) plot(weight ~ tall, data=df, pch=21, col='skyblue',bg='skyblue', cex=1.5) #3. 단순회귀 분석하기 #절편: 3.69841 / 기울기:-0.04754 model <- lm(weight ~ tall, data=df) model # 4. 2번에서 시각화한 산포도 그래프에 회귀직선 겹쳐 그리기 attch(df) plot(weight ~ tall, data=df, pch=21, col='skyblue',bg='skyblue', cex=1.5) model <- lm(weight ~ tall, data=df) abline(model, col='red') title('키가 체중에 미치는 영향') #5. 단순회귀분석 결과 해석하기 options(scipen=999) #0.00000 이런식으로 보기위함 summary(model)회귀방정식: 체중= -132.948 +1.146 * 키
해석: 키가 1cm 증가할때 체중이 평균적으로1.146kg증가한다.
실습 5. 평수당 집값예측하는 단순 회귀 분석을 수행하시오.
출처. 서울시 부동산데이터
#1. 데이터 불러오기 house <- read.csv("c:\\data\\house.csv",header =T, fileEncoding ='euc-kr') house head(house) #2. 데이터로 산포도 그래프 그리기 attch(house) plot(물건금액 ~ 건물면적, data=house, pch=21, col='orange',bg='yellow', cex=1.5) #3. 단순회귀 분석하기 #절편: / 기울기: model <- lm(물건금액 ~ 건물면적, data=house) model # 4. 2번에서 시각화한 산포도 그래프에 회귀직선 겹쳐 그리기 attch(house) plot(물건금액 ~ 건물면적, data=house, pch=21, col='orange',bg='yellow', cex=1.5) model <- lm(물건금액 ~ 건물면적, data=house) abline(model, col='red') title('건물면적이 물건금액에 미치는 영향') #5. 단순회귀분석 결과 해석하기 options(scipen=999) #0.00000 이런식으로 보기위함 summary(model)
회귀방정식: 물건금액= 18032.5 + 913.5* 건물면적
해석: 건물면적이 1제곱미터 증가할때 물건금액이 평균적으로 913.5 만원 증가한다.
실습 6 : 혼인건수에 따른 유아용품에 대한 회귀분석
#1. 데이터 불러오기 a <- read.csv("c:\\data\\회귀분석.csv",header =T, fileEncoding ='euc-kr') a head(a) #2. 데이터로 산포도 그래프 그리기 attch(a) plot(CHIL~MARRY_COUNT , data=a, pch=21, col='orange',bg='yellow', cex=1.5) #3. 단순회귀 분석하기 #절편: / 기울기: model <- lm(CHIL~MARRY_COUNT , data=a) model # 4. 2번에서 시각화한 산포도 그래프에 회귀직선 겹쳐 그리기 attch(a) plot(CHIL~MARRY_COUNT , data=a, pch=21, col='orange',bg='yellow', cex=1.5) model <- lm(CHIL~MARRY_COUNT , data=a) abline(model, col='red') title('혼인건수가 유아용품수에 미치는 영향') #5. 단순회귀분석 결과 해석하기 options(scipen=999) #0.00000 이런식으로 보기위함 summary(model)
회귀방정식: 유아용품수= 690.88+ 35.22* 혼인건수
해석: 혼인건수가 1건이 증가할때 유아용품수가 평균적으로 35.22개 증가한다.
+ p-value가 0.05보다 작기 때문에 혼인건수와 유아용품수와의 관계가 유의미하다.
'빅데이터 분석(with 아이티윌) > R' 카테고리의 다른 글
| [빅데이터분석] R _ 60. 다중회귀 (0) | 2024.07.18 |
|---|---|
| [빅데이터분석] R _ 59. 상관관계 (0) | 2024.07.16 |
| [빅데이터분석] R _ 57. 의사 결정 트리 (5) | 2024.07.16 |
| [빅데이터분석] R _ 56. 규칙기반 알고리즘(one r/riper 알고리즘) (0) | 2024.07.12 |
| [빅데이터분석] R _ 55. 하이퍼 파라미터 (1) | 2024.07.12 |




















